Star Raiders¶
The Problem¶
The classic game Star Raiders was written in 1979 by Doug Neubauer and became a killer app for the original Atari 400/800 computer system. It’s a seminal game.

An issue that you notice playing it is that the framerate slows down considerably when an explosion occurs. This is because the explosions are rendered as a bunch of individual points expanding in the 3D coordinate space, and converting to the 2D screen representation requires lots of math. The 6502 has no built-in division operation, and in an interview with James Hague, Doug Neubauer stated that his signed division code was not optimal.
So, that’s my starting point: see if I can replace the division algorithm with something faster.
Oct 20, 2015: Star Raiders Source Code!¶
In an unexpected twist, an original paper copy of the Star Raiders source was discovered by Steve Hales, scanned by Kevin Savetz, and placed on the Internet Archive.
It’s commented! Understatement of the day: that makes it much easier to understand the code! As an example: in my Jul 26th entry, I said it appeared there was an 18 byte “structure” with 49 entries, but I had no idea what the individual structure might look like. In the source code, it shows that there are indeed 49 entries (RAMNUM):
STRNUM = 12 ; NUMBER OF STARS DISPLAYED
OBJNUM = 5 ; NUMBER OF OBJECTS
EXPNUM = 32 ; NUMBER OF EXPLOSION STARS
RAMNUM = OBJNUM+STRNUM+EXPNUM ; TOTAL NUMBER OF RAM :
and here’s the structure (note: 18 bytes!):
STRRAM: ; RAM FOR STARS , OBJECTS POSITIONS, ETC.
XSIGN: ; SIGN OF XPOS
.res RAMNUM
YSIGN:
.res RAMNUM
ZSIGN:
.res RAMNUM
XPOSH: ; XPOS IN SPACE HI BYTE
.res RAMNUM
YPOSH:
.res RAMNUM
ZPOSH:
.res RAMNUM
XPOSL: ; XPOS IN SPACE LO BYTE
.res RAMNUM
YPOSL:
.res RAMNUM
ZPOSL:
.res RAMNUM
XINCRE: ; OBJECTS X DIRECTION VELOCITY
.res RAMNUM
YINCRE:
.res RAMNUM
ZINCRE:
.res RAMNUM
VPOS: ; VERT POS ON SCREEN
.res RAMNUM
HPOS: ; HORIZ POS ON SCREEN
.res RAMNUM
OLDVER: ; OLD VERT POSIT
.res RAMNUM
GINDEX: ; TYPE OF GRAPHIC: OBJECT
OLDHOR: ; OLD HORIZ POSIT: STARS
.res RAMNUM
OLDNUM: ; PREVIOUS NUMBER OF BYTES
OLDBYT: ; OLD BYTE IN RAM MAP
.res RAMNUM
NUMBYT: ; HOW MAY BYTES TO STORE: OBJCET
STRBYT: ; THE BYTE TO STORE: STARS
.res RAMNUM
Nice to have the structure all defined like that instead of having to reverse engineer it! There’s also a comment describing how the fixed point arithmetic is defined:
; UNIVERSE LOOKS LIKE SIGN HI BYTE LOW:
; -INFINITY = 00 00 00
; 0 = 01 00 00
; +INFINITY = 01 FF FF
; -1 = 00 FF FF
Jul 31, 2015: Retrochallenge Summary¶
The Retrochallenge is over and I was not able to finish my project. However, I did make progress and have a clear idea of the solution, if no idea on how to actually implement it or where to put it in the code or how the code actually uses its current division algorithm.
Stay tuned to this page for infrequent updates, and perhaps as my entry into the Retrochallenge 2016/01!
Jul 26, 2015: Debugging Help¶
The WUDSN IDE has source level debugging when using the MADS assembler, but unfortunately I’m not using the MADS assembler and haven’t investigated how hard it would be to convert the CC65 assembler format to MADS. Probably not insurmountingly hard, but I’m not taking that direction at this point because I hate Eclipse. Kinda stupid to hate tools, but it’s always been miserable to set up for me, and plus: Java.
Altirra does have a nice graphical debugger and I finally started to understand (using VirtualBox – wine seems a bit flaky).
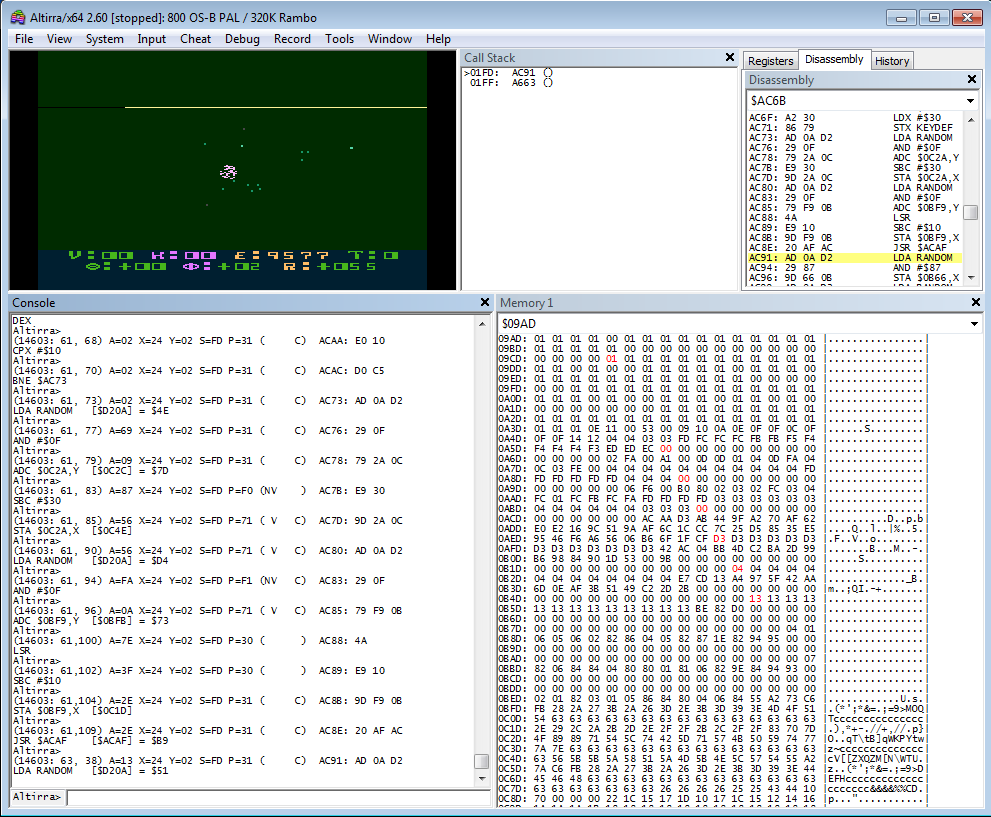
Using F8 to break into the program, I set a breakpoint at $AC6B which is
the assembled location of INIT_EXPLODE in the starraiders.lst output
file. Then use F8 to restart and wait for an explosion.
Interestingly (and frustratingly for debugging purposes!) I’ve found that if you fly the ship straight, the enemies do this oddball orbit around you, firing all the time, but the shots miss most of the time.
Once you do manage to get an explosion, the breakpoint is triggered and the arrays that I think are for the explosion data are filled up. INIT_EXPLODE loops $20 times (from $30 down to $10) to fill the following arrays:
SUB91: lda $09AD,y
sta $09AD,x
lda $0A40,y
sta $0A40,x
lda $0AD3,y
sta $0AD3,x
SUB90: lda $09DE,y
sta $09DE,x
lda $0A71,y
sta $0A71,x
lda $0A0F,y
sta $0A0F,x
lda $0AA2,y
sta $0AA2,x
lda $0B04,y
sta $0B04,x
lda $0B35,y
sta $0B35,x
RTS90: rts
Have no idea what these arrays are for, yet, but using the Memory window of
Altirra I can see them changing. So stuff is happening at least.
I’m guessing there’s a “structure” with 49 records of 18 bytes each. This is a structure in the 6502 sense, laid out in groups of 49 consecutive bytes that represent the same field in the structure, rather than interleaved as a C structure would be. Here’s an example of a C structure:
struct {
byte a, b, c, d, e;
};
struct test[8];
and its 40 byte layout in memory (at an arbitrary memory location $1000):
1000: abcdeabcdeabcdea
1010: bcdeabcdeabcdeab
1020: cdeabcde
but for 6502 efficiency, you’d like this laid out differently:
1000: aaaaaaaabbbbbbbb
1010: ccccccccdddddddd
1020: eeeeeeee
In this 6502-optimized structure layout, to access a particular element of
the structure, say test[2], you’d set an index register, say x, to 2 and
access all the elements of a particular record using that same index:
ldx #2 ; interested in record 2
lda $1000,x ; test[2].a
lda $1008,x ; test[2].b
lda $1010,x ; test[2].c
lda $1018,x ; test[2].d
lda $1020,x ; test[2].e
If this were arranged in the normal C style, you’d have to access test[2] by first finding the offset to the first element of that record by multiplying by the record length (5, in this case) as in:
ldx #2 ; interested in record 2
txa ; start mult by 5
sta $80 ; save value to some temp location
asl ; *2
asl ; *2 again (so *4 cumulatively so far)
clc
adc $80 ; add orig value again (so *5 cumulatively)
tax ; and stuff it back into the index register
lda $1000,x ; test[2].a
lda $1001,x ; test[2].b
lda $1002,x ; test[2].c
lda $1003,x ; test[2].d
lda $1004,x ; test[2].e
In addition to the speed penalty for laying things out in C standard order, there is also a size restriction resulting from this (naive) implementation: the total size can’t be larger than 255 + len(struct test) bytes because the x register can of course only contain a single byte. Of course bigger structures are possible but that involves more computations at each access.
Back to Star Raiders: looking at the source there are a bunch of references to various memory locations offset using the X register – starting at $09ad, and increasing by #49 until $0d1f which the source indicates is:
STATUS_LINE = $D1F ; status line holding text
So, using Python, I find these addresses:
>>> for i in range(19):
... print i, hex(0x9ad + 49*i)
...
0 0x9ad
1 0x9de
2 0xa0f
3 0xa40
4 0xa71
5 0xaa2
6 0xad3
7 0xb04
8 0xb35
9 0xb66
10 0xb97
11 0xbc8
12 0xbf9
13 0xc2a
14 0xc5b
15 0xc8c
16 0xcbd
17 0xcee
18 0xd1f
Ok. Progress. But, what sorts of values does each of those store?
I’m going to bed. 4am I am not.
Jul 17, 2015: Understanding Division Algorithms¶
OK, so I’m struggling with the debuggers in both atari800 and Altirra and I’m having a hard time making progress with the Star Raiders because I have to wait for an explosion to set a breakpoint, which means a minute or two to fly around, find some Zylons and shoot one to generate an explosion. Lots of time for each iteration. I’m pretty close to abandoning the project for the time being (again).
But, here at KansasFest I bought the book Assembly Lines from the editor of the book, Chris Torrence, and got to wondering how the division algorithm (below, from codebase64) might work. So here’s a dissection.
Here’s the code again, this time modified for MAC/65 with an infinite loop such that I can break into it in the debugger, set the carry, set a breakpoint at 203c, and step through the code to grab the memory locations for the dividends and divisors:
*= $02E0
.WORD INIT
*=$2000
dividend = $80 ;$81 used for hi-byte
divisor = $82 ;$83 used for hi-byte
remainder = $84 ;$85 used for hi-byte
result = dividend ;save memory by reusing divident to store the result
init lda #$6D ; %01101101
sta dividend
lda #$DB ; %11011011
sta dividend+1
lda #$38 ; %10011100
sta divisor
lda #$05 ; %00000010
sta divisor+1
clc
wait bcc wait
jsr divide
jmp init
divide lda #0 ;preset remainder to 0
sta remainder
sta remainder+1
ldx #16 ;repeat for each bit: ...
divloop asl dividend ;dividend lb & hb*2, msb -> Carry
rol dividend+1
rol remainder ;remainder lb & hb * 2 + msb from carry
rol remainder+1
lda remainder
sec
sbc divisor ;substract divisor to see if it fits in
tay ;lb result -> Y, for we may need it later
lda remainder+1
sbc divisor+1
bcc skip ;if carry=0 then divisor didn't fit in yet
sta remainder+1 ;else save substraction result as new remainder,
sty remainder
inc result ;and INCrement result cause divisor fit in 1 times
skip dex
bne divloop
rts
As a refresher (and I had to look this up myself again), the divisor is what you’re dividing by. In fractional terms, the dividend is the numerator and the divisor is the denominator.
It looks like this algorithm is looping through 16 times:
Dividend Remainder Divisor
H L H L H L
11011011 01101101 00000000 00000000 00000010 10011100 Initial X=16
10110110 11011010 00000000 00000001 00000010 10011100
01101101 10110100 00000000 00000011 00000010 10011100
11011011 01101000 00000000 00000110 00000010 10011100
10110110 11010000 00000000 00001101 00000010 10011100
01101101 10100000 00000000 00011011 00000010 10011100
11011011 01000000 00000000 00110110 00000010 10011100
10110110 10000000 00000000 01101101 00000010 10011100
01101101 00000000 00000000 11011011 00000010 10011100
11011010 00000000 00000001 10110110 00000010 10011100
10110100 00000001 00000000 11010001 00000010 10011100
01101000 00000010 00000001 10100011 00000010 10011100
11010000 00000101 00000000 10101010 00000010 10011100
10100000 00001010 00000001 01010101 00000010 10011100
01000000 00010101 00000000 00001111 00000010 10011100
10000000 00101010 00000000 00011110 00000010 10011100
00000000 01010100 00000000 00111101 00000010 10011100 X=0
so the final result of 0xdb6d/0x029c is 0x54 with a 0x3d remainder.
Jul 14, 2015: Logarithms!¶
Arrived at KansasFest with the intent of working on Star Raiders as my bandit entry into the Hackfest challenge. (Unlikely they will actually accept an Atari entry, but we’ll just say it’s a parallel challenge.)
I talked to Martin Haye, co-author of Lawless Legends and he suggested lookup tables using logarithms to speed up the division, which is one of those things that in hindsight should have been obvious. He said that for the cost of the log table and its inverse (the exponential function), he can get an approximate division result with only a couple of shifts and subtraction – stuff that the 6502 can do well.
So, that’s my new approach: logs. I need to figure out how the variables are being passed into the current division algorithm and what the range of the results are, and then I can start generating log tables.
Jul 1, 2015: Retro-Challenge¶
I was reminded about the Retro Challenge while listening to the latest RCR Podcast and thought it would be a perfect way to motivate me to start looking at Star Raiders again. The Retro Challenge goes through the month of July, but I expect that I’ll be doing most of my work during KansasFest while other people are working on their Apple Hackfest projects.
Mar 23, 2015: Pre Retro-Challenge¶
I have no idea what I’m doing.
I’m going to walk you through my process as I try to figure things out.
The first $200 bytes of source is commented by someone, presumably Sidney
Cadot, the person I forked the source from. The rest is largely uncommented,
but whatever program did the disasssembly did a pretty good job of creating
local loop variables and stuff. (Local loops meaning the equivalent of a
for loop or something, not a jump target from outside the soubroutine – e.g.
some loop within the subroutine.)
Looking through to try to find the division algorithm, I didn’t have any idea really what a division algorithm should look like, so I found an example 16 bit division algorithm on codebase64.org, which I reproduce here:
divisor = $58 ;$59 used for hi-byte
dividend = $fb ;$fc used for hi-byte
remainder = $fd ;$fe used for hi-byte
result = dividend ;save memory by reusing divident to store the result
divide lda #0 ;preset remainder to 0
sta remainder
sta remainder+1
ldx #16 ;repeat for each bit: ...
divloop asl dividend ;dividend lb & hb*2, msb -> Carry
rol dividend+1
rol remainder ;remainder lb & hb * 2 + msb from carry
rol remainder+1
lda remainder
sec
sbc divisor ;substract divisor to see if it fits in
tay ;lb result -> Y, for we may need it later
lda remainder+1
sbc divisor+1
bcc skip ;if carry=0 then divisor didn't fit in yet
sta remainder+1 ;else save substraction result as new remainder,
sty remainder
inc result ;and INCrement result cause divisor fit in 1 times
skip dex
bne divloop
rts
and again, I have no idea what I’m doing, but I noticed that there was a
ASL followed by a ROL, which only happens in two places in the code:
SUB65 and SUB73
As an aside, if you want to read about someone who knows about reverse engineering, check out 4am on twitter who has some really technical but very entertaining writeups.
So:
SUB73seems more likely candidate for arbitrary division becauseSUB65isn’t a loop, it drops straight through.variable
$79seems to hold counterSUB89(renamed to INIT_EXPLODE) seems to set initial params for explosion because these are the same data storage places referenced inSUB73(andSUB65) for that matter.
I set a break point at $AC6B and fired up Star Raiders, went to galactic
chart, hyperspaced, started attacking soemthing, got a hit, and blam! The
breakpoint was triggered. Seems like it might be right.
This bit of code might be where the explosion data is saved:
SUB91: lda $09AD,y
sta $09AD,x
lda $0A40,y
sta $0A40,x
lda $0AD3,y
sta $0AD3,x
